Solving the Selection Problem using a Heap
In this post, I am going to describe the heap data structure, and use it solve the selection problem:
given an array of length n, and an integer \(k \le n\), return the kth largest number in the array.
An obvious solution would be to sort the array and take the kth element. The time complexity of this solution is \(O (n \log n)\); with the help of a heap, we can do it faster. I’ll describe two ways to do it, in either \(O (n + k \log k)\) time, or \(O (k + (n-k) \log k)\) time.
A Max Heap
A Max Heap is a binary tree satisfying two properties:
- Shape property: it is a complete binary tree, meaning that all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
- Heap property: each node’s value is greater than or equal to its children’s values.
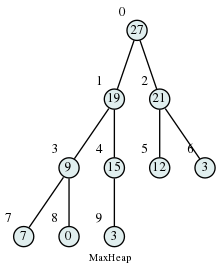
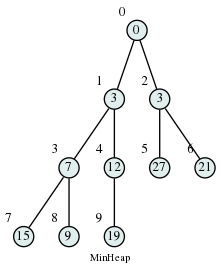
Replacing “greater” with “smaller” in this definition results in a Min Heap:
A Max Heap of \(n\) elements can be created in \(O(n)\) time and allows to:
- find maximum in \(O(1)\) time
- pop the maximum element in \(O(\log n)\) time
- insert a new element in \(O(\log n)\) time
- increase a key in $$O(\log n) time
Binary heaps are usually implemented as arrays, which saves the overhead cost of storing pointers to child and parent nodess. The number above the node in the picture is the corresponding index of the array. The left child of element number n will have index \(2*n+1\), the right child - \(2*n+2\), its parent - \(\lfloor (n-1)/2 \rfloor\).
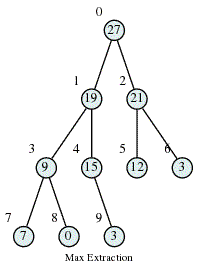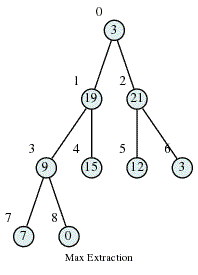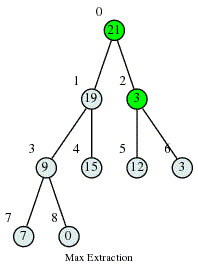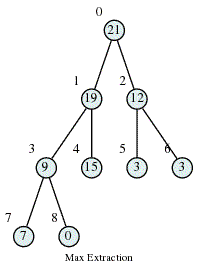
Max Heap Deletion Algorithm
Step 1 − Remove root node. Step 2 − Move the last element of last level to root. Step 3 − If the inserted node is smaller than one of its children, swap it with the largest child. Step 4 − Repeat step 3 until Heap property holds.
Max Heap Construction Algorithm
We could insert elements one by one, but that would take \(O(n \log n)\) time. Instead, we “heapify” the tree from the bottom layer to the top. For every node we ensure that it’s bigger than both of its children, and if it isn’t, we do the same thing as in the Heap Deletion algorithm: swap it with the largest child until Heap property holds.
How long does this take? There are no more than n/2 nodes at the second-lowest level, n/4 at the next level, and so on. So the total number of swaps is no more than \(1 \frac{n}{2} + 2 \frac{n}{4} + 3 \frac{n}{8} + \ldots = 2n = O(n)\).
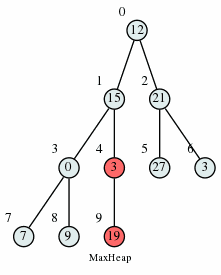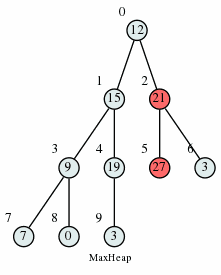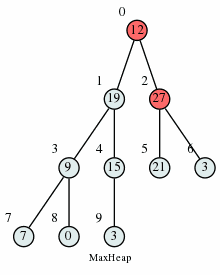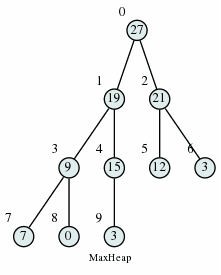
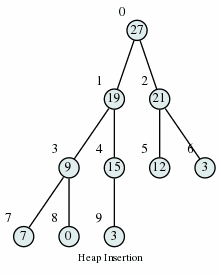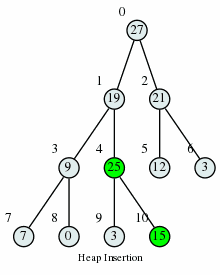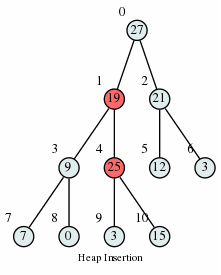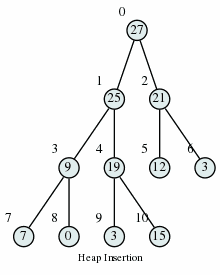
Max Heap Insertion Algorithm
Step 1 − Create a new node at the end of heap. Step 2 − Assign new value to the node. Step 3 − Compare the value of this child node with its parent. Step 4 − If value of parent is less than child, then swap them. Step 5 − Repeat step 3 & 4 until Heap property holds.
Here is my implementation of a heap in Python:
class MaxHeap:
def __init__(self, nums):
self.n = len(nums)
self.nums = list(nums)
for i in reversed(range(1, self.n // 2 + 1)):
self.MaxHeapify(i)
def left(self, i):
return 2*i + 1
def right(self, i):
return 2*i + 2
def parent(self, i):
return (i-1) // 2
def MaxHeapify(self, i):
"""Assuming that left and right subtrees of i are
already heaps, heapify the subtree rooted at i"""
l = self.left(i)
r = self.right(i)
if l < self.n and self.nums[l] > self.nums[i]:
largest = l
else:
largest = i
if r < self.n and self.nums[r] > self.nums[largest]:
largest = r
if largest != i:
self.nums[i], self.nums[largest] = self.nums[largest], self.nums[i]
self.MaxHeapify(largest)
def IncreaseKey(self, i, val):
assert val >= self.nums[i]
self.nums[i] = val
while i > 1 and self.nums[i] > self.nums[self.parent(i)]:
self.nums[i], self.nums[self.parent(i)] = self.nums[self.parent(i)], self.nums[i]
i = self.parent(i)
def Insert(self, val):
self.n += 1
if len(self.nums) < self.n:
self.nums.append(val)
else:
self.nums[self.n-1] = val
self.IncreaseKey(self.n-1, val)
def ExtractMax(self):
assert self.n > 1
ans = self.nums[0]
self.nums[0] = self.nums[self.n-1]
self.n -= 1
self.MaxHeapify(0)
return ansSolving the selection problem
In Python, a min heap is implemented in a heapq module from Python standard library. A min heap can simulate a max heap if we multiply all elements by -1.
Back to our problem: given an array of length n, and an integer \(k \le n\), return the kth largest number in the array.
One solution is to create a min heap to store k largest elements as we go through the array. It takes \(O(k)\) time create a heap out of the first k elements, and (in the worst case) \(O(\log k)\) to deal with each of the remaining \(n-k\) elements, so this algorithm takes \(O(k + (n-k) \log k)\) time:
import heapq
def findKthLargest(nums: List[int], k: int) -> int:
heap = nums[:k].copy()
heapq.heapify(heap)
for num in nums[k:]:
if num > heap[0]:
heapq.heapreplace(heap, num)
return heap[0]This is basically what heapq.nlargest function does, except that it also sorts the output, and we don’t need that.
We could solve this problem differently:
- Turn the whole array into a max heap, and insert its root into an auxiliary max heap.
- k-1 times pop an element from the second heap, and push back its children from the first heap.
- Return the root of the second heap.
import heapq
def findKthLargest(nums: List[int], k: int) -> int:
x = [-t for t in nums]
heapq.heapify(x)
s = [(x[0], 0)] #auxiliary heap
for _ in range(k-1):
ind = heapq.heappop(s)[1]
if 2*ind+1 < len(x):
heapq.heappush(s, (x[2*ind+1], 2*ind+1))
if 2*ind+2 < len(x):
heapq.heappush(s, (x[2*ind+2], 2*ind+2))
return -s[0][0]This algorithm takes \(O(n + k\log k)\) time, and \(O(n + k)\) additional space if we are not allowed to modify the given array. Which one is faster depends on values of k and n, and on constants in the big O. For Leetcode challenge, the first one was faster.
The second algorithm was proposed by Frederickson as a first step to his more complicated algorithm that can select a kth element from a heap in \(O(k)\) time[2]. Using Frederickson’s algorithm, we could solve the selection problem in O(n+k) time. That would be an overly complicated and suboptimal solution to the problem, though, because in the next post we will see that selecting the kth element from an array can be done in \(O(n)\) worst-case time.
Resources:
[1] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4., pp.151-169
[2] Frederickson, Greg N. “An optimal algorithm for selection in a min-heap.” Information and Computation 104.2 (1993): 197-214.